Power Network System tutorial

Overview

In this tutorial you will:
  • Model the HYCON2 benchmark "Power Network System" (see PnPMPC toolbox v0.9 manual for details).
  • Build the H2T object and use it to check and set parameters required for PnPMPC and MPT toolboxes.
  • Use H2T object to build decentralized PnPMPC controllers.
  • Use h2T object to build two MPT controllers with different level of aggression, and compare closed-loop trajectories.

Requirements


The example is available in the Examples/PNS folder of the toolbox.
Run
showdemo PNS_start
to open it, or
echodemo PNS_start
for an interactive demo.

Step 1 
Power Network System Model

  • Download problem data (download link), and extract the four .mat files in the current Matlab directory.
  • Load state-space A, B, C, D matrices for the 4 Areas:
load('PNS_SS_matrices');
  • Create a cell array of state-space discrete systems with sampling time 1s:
for i = 1:4
    sys{i} = c2d(ss(A{i},B{i},C{i},D{i}),1);
end
  • Add signal names (IMPORTANT. LSmodel class uses signal names to find interconnections and set signal limits):
load('PNS_signal_names');

for i = 1:4
    sys{i}.InputName = name_inputs{i};
    sys{i}.StateName = name_states{i};
    sys{i}.OutputName = name_states{i};
end
  • Build the LSmodel from the SS representation, specifying external inputs and outputs (internal connections are automatically generated by matching signal names):
model = LSmodel(sys, 0, name_external_inputs, name_external_outputs)
  • Add signal limits with the set_sig_lim method, passing signal name, lower bound, and upper bound as arguments:
load('PNS_signal_limits');

for i = 1:length(name_external_inputs)/2
    model = model.set_sig_lim(name_external_inputs((i-1)*2+1),-DrefMIN(i),DrefMAX(i));
end

for i = 1:length(name_external_outputs)/4
    model = model.set_sig_lim(name_external_outputs((i-1)*4+1),-DtetaMIN(i),DtetaMAX(i));
end

Step 2
H2T object and control parameters

To start from this step, download the complete system model (download link).

  • Build H2T object passing the model as argument to the constructor:
h2t_obj = h2t(model)
  • Check parameters required by the PnPMPC toolbox: 
h2t_obj.checkParameters('PnPMPC')
You will see that the following parameters are missing:
  1. required: prediction horizon, k, input and output types;
  2. facultative: YALMIP settings.
  • For an explanation about their meaning, check the following PnPMPC help page: 
help createCtrlPnPMPC4lsmodel
  • Load parameters from problem data:
load('PNS_control_parameters')
  • Set generic parameters:
h2t_obj.setParameters('PredictionHorizon', N, 'StateWeights', Q, 'InputWeights', R)
Note how weights can be passed as scalar. In this case the weight will be automatically multiplied by an identity matrix of proper dimensions.
  • Set PnPMPC-related parameters:
h2t_obj.setParameters('k', k, 'm', m, 'p', p, 'sdpsettings', sdp)
  • Check parameters required by the MPT toolbox: 
h2t_obj.checkParameters('MPT')
You will see that no additional parameters are required to build the MPT controller.

Step 3
PnPMPC decentralized controllers

To start from this step, download the complete H2T object (download link).

  • Build PnPMPC controllers (if you get a Java Exception here, just run command again):
ctrl_pnpmpc = h2t_obj.buildController('PnPMPC')
You will get an array of four controller objects, one for each Area of the Power Network System.
  • Set zero-terminal constraint:
for i = 1:4
    ctrl_pnpmpc(i) = ctrl_pnpmpc(i).zeroTerminal(Q((1:4),(1:4)), R)
end
  • Controllers are now ready, and can be used to compute the control action for a given system state:
x = .05*rand(4,1)
u = ctrl_pnpmpc(1).uRH( x )

Step 4
MPT soft and aggressive controllers

To start from this step, download the complete H2T object (download link).

  • Set weights for soft controller:
h2t_obj.setParameters('StateWeights', 1, 'InputWeights', 1)
  • Build soft MPT controller:
ctrl_mpt_soft = h2t_obj.buildController('MPT')
MPT object comes with the simulate method to easily perform closed-loop simulations.
  • Perform a 15-seconds closed-loop simulation starting from a random initial condition:
x0 = 0.1*rand(16,1);
closedloop_data_soft = ctrl_mpt_soft.simulate(x0, 15)
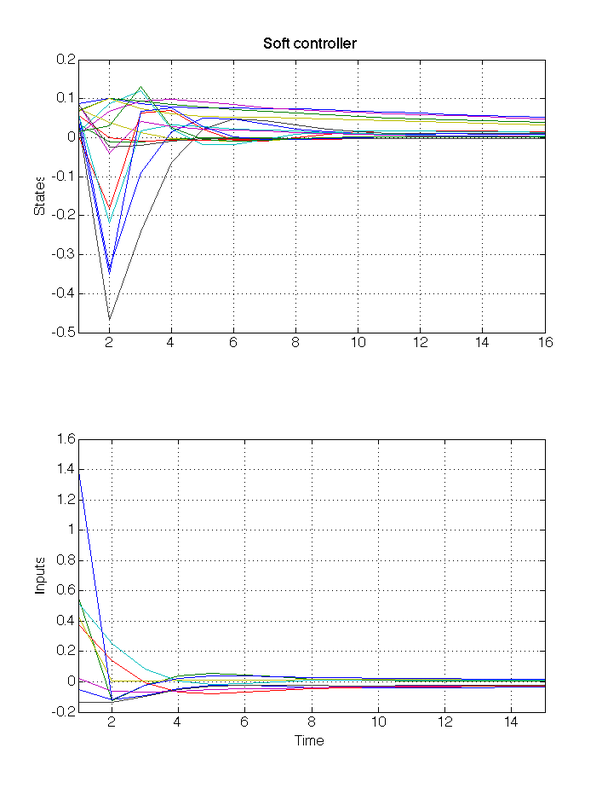
Plot state and input trajectories:
figure(1), subplot(211)
plot(closedloop_data_soft.X')
title('Soft controller'), ylabel('States')

subplot(212)
plot(closedloop_data_soft.U')
ylabel('Inputs'), xlabel('Time')
  • Change parameters and build a more aggressive controller:
h2t_obj.setParameters('StateWeights', 10, 'InputWeights', 0.1)
ctrl_mpt_aggressive = h2t_obj.buildController('MPT')
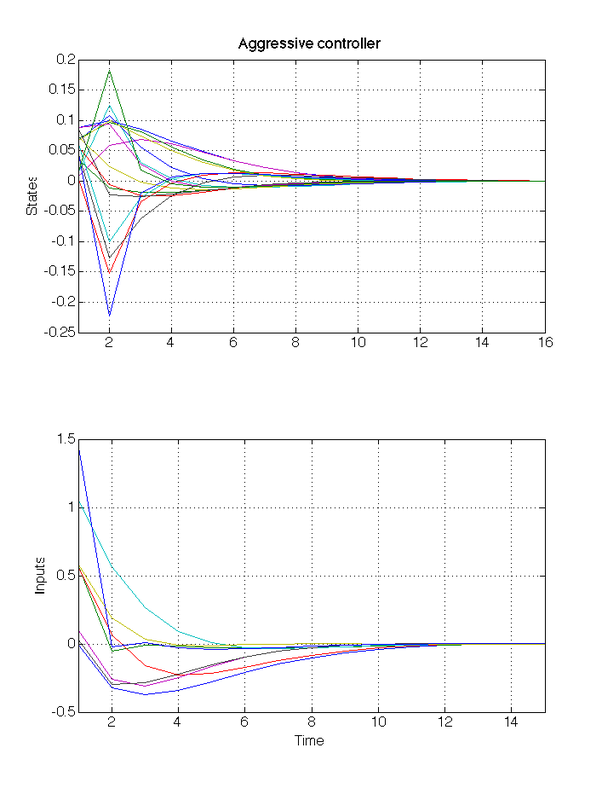
  • Perform a new closed-loop simulation and plot the results:
closedloop_data_aggressive = ctrl_mpt_aggressive.simulate(x0, 15)


figure(2), subplot(211)
plot(closedloop_data_aggressive.X')
title('Aggressive controller'), ylabel('States')

subplot(212)
plot(closedloop_data_aggressive.U')
ylabel('Inputs'), xlabel('Time')
At the end, you should get something similar to the following figures.