Masses tutorial

Overview

In this tutorial you will:
  • Model a system composed by a set of masses serially connected by springs and dampers, with two fixed walls at the far ends, and with actuators exerting forces between each pair.
  • Build the H2T object and use it to check and set parameters required for MPT and PnPMPC toolboxes.
  • Use H2T object to build the MPT and PnPMPC controllers.
  • Compare the open-loop evolutions with the closed-loop trajectories driven by the two controllers.

Requirements


The example is available in the Examples/Masses folder of the toolbox.
Run
showdemo Masses_start
to open it, or
echodemo Masses_start
for an interactive demo.

Step 1 
System Model

  • Set physical parameters, where 'M' is the number of masses, 'm' is the mass, 'k' and 'c the spring and damping coefficients, respectively:
M = 3; , m = 1; , k = 1.5; , c = 1;
  • Set the number of states (position and velocity for each mass) and the number of inputs:
nx = 2*M; , nu = M-1;  
  • Build the continuous-time matrices:
Ac = full( [zeros(M,M) eye(M) gallery('tridiag',M,k/m,-2*k/m,k/m) gallery('tridiag',M,c/m,-c*k/m,c/m)] );
Bc = full( [zeros(M,M-1); gallery('tridiag',M-1,-1/m,1/m,0); zeros(1,M-2) -1/m] );
Cc = eye(nx);
  • Create the standard SS system object discretizing with 0.5s sampling time:
sys = c2d( ss(Ac, Bc, Cc, 0), 0.5)
  • Add signal names to the InputName, StateName and OutputName attributes of the standard SS object:
for i = 1:nu
    sys.InputName(i) = { strcat('actuator', int2str(i)) };
end

for i = 1:M
    sys.StateName(i) = { strcat('pos', int2str(i)) };
    sys.OutputName(i) = { strcat('pos', int2str(i)) };
end

for i = (M+1):nx
    sys.StateName(i) = { strcat('vel', int2str(i-M)) };
    sys.OutputName(i) = { strcat('vel', int2str(i-M)) };
end

  • Build the LSmodel object passing the external inputs and outputs names, which in this case coincide with the input and state names, respectively:
model = LSmodel(sys, sys.InputName, sys.StateName);
  • Add signal limits with set_sig_lim method by matching signal names (for this example, we want to bound inputs between +1 and -1, and states between +4 and -4):
for i = 1:nu
    model = model.set_sig_lim(strcat('actuator', int2str(i)), -1, 1);
end

for i = 1:M
    model = model.set_sig_lim(strcat('pos', int2str(i)), -4, +4);
end

for i = M+1:nx
    model = model.set_sig_lim(strcat('vel', int2str(i-M)), -4, +4);
end

Step 2
H2T object and control parameters

To start from this step, download the complete system model (download link).

  • Build H2T object passing the model as argument to the constructor:
h2t_obj = h2t(model)
  • Set prediction horizon and weights:
h2t_obj.setParameters('PredictionHorizon', 10, 'StateWeights', 1, 'InputWeights', 0.1)
Note how weights can be passed as scalar. In this case the weight will be automatically multiplied by an identity matrix of proper dimensions.

Step 3
Open-loop simulation

To start from this step, download the H2T object (download link) and the State-Space representation (download link).

  • Initialize simulation data:
Tsim = 50;
x = zeros(nx,Tsim); , x(:,1) = [3 -2 1 0 0 0]';
u = zeros(nu,Tsim);
  • Open-loop evolution:
for i = 2:Tsim 
    x(:,i) = sys.A*x(:,i-1) + sys.B*u(:,i-1);    
end
  • Plot results:
figure(1), subplot(211)
hold on
plot(x(1,:)), plot(x(2,:),'r'), plot(x(3,:),'k')
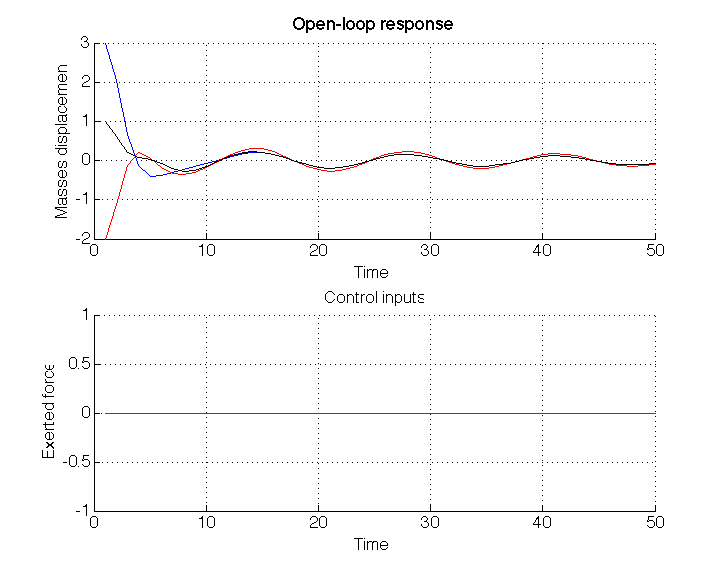
title('Open-loop response'), xlabel('Time'), ylabel('Masses displacement')

subplot(212)
hold on
plot(u(1,:)), plot(u(2,:),'r')
title('Control inputs'), xlabel('Time'), ylabel('Exerted force')
You should get something similar to the following figure.
Immagine

Step 4
MPT controller

To start from this step, download the H2T object (download link) and the State-Space representation (download link).

  • Check parameters for MPT controller:
h2t_obj.checkParameters('MPT');
You should see that all parameters are ready.
  • Build MPT controller:
ctrlMPT = h2t_obj.buildController('MPT');
  • Initialize simulation data:
Tsim = 50;
x = zeros(nx,Tsim); , x(:,1) = [3 -2 1 0 0 0]';
u = zeros(nu,Tsim);
  • Run closed loop simulation, computing the control input with the evaluate method of the MPT controller object:
for i = 2:Tsim  
    u(:,i-1) = ctrlMPT.evaluate(x(:,i-1));   
    x(:,i) = sys.A*x(:,i-1) + sys.B*u(:,i-1); 
end
Plot state and input trajectories:
figure(2), subplot(211)
hold on
plot(x(1,:)), plot(x(2,:),'r'), plot(x(3,:),'k')
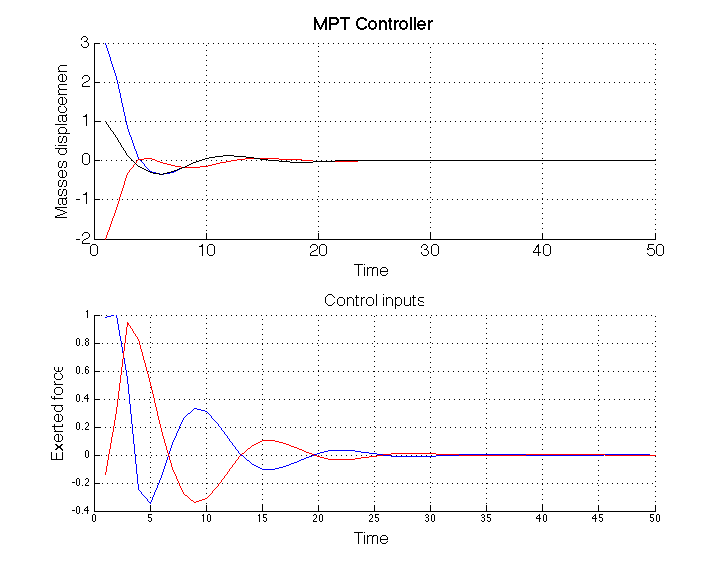
title('MPT Controller'), xlabel('Time'), ylabel('Masses displacement')

subplot(212)
hold on
plot(u(1,:)), plot(u(2,:),'r')
title('Control inputs'), xlabel('Time'), ylabel('Exerted force')
You should get something similar to the following figure.
Immagine

Step 5
PnPMPC controller

To start from this step, download the H2T object (download link) and the State-Space representation (download link).

  • Check parameters for PnPMPC controller:
h2t_obj.checkParameters('MPT');
  • Set missing parameters (for an explanation of their meaning type 'help createCtrlPnPMPC4lsmodel'):
h2t_obj.setParameters('k', {10}, 'm', ones(nu,1) ,'p', ones(nx,1))
  • Build PnPMPC controller and set zero-terminal constraint (if you get a Java Exception, simply run command again):
ctrlPnPMPC = h2t_obj.buildController('PnPMPC');
ctrlPnPMPC = ctrlPnPMPC.zeroTerminal(eye(nx), eye(nu));
  • Initialize simulation data:
Tsim = 50;
x = zeros(nx,Tsim); , x(:,1) = [3 -2 1 0 0 0]';
u = zeros(nu,Tsim);
  • Run closed loop simulation, computing the control input with the uRH method of the PnPMPC controller object:
for i = 2:Tsim  
    u(:,i-1) = ctrlPnPMPC.uRH(x(:,i-1));   
    x(:,i) = sys.A*x(:,i-1) + sys.B*u(:,i-1);  
end
Plot state and input trajectories:
figure(3), subplot(211)
hold on
plot(x(1,:)), plot(x(2,:),'r'), plot(x(3,:),'k')
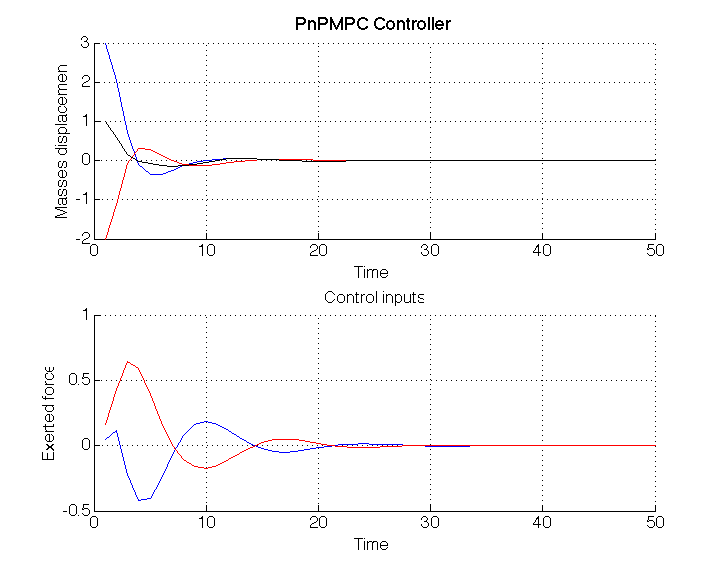
title('PnPMPC Controller'), xlabel('Time'), ylabel('Masses displacement')

subplot(212)
hold on
plot(u(1,:)), plot(u(2,:),'r')
title('Control inputs'), xlabel('Time'), ylabel('Exerted force')
You should get something similar to the following figure.
Immagine