Recursive
Compressed Sensing

Recursive Compressed Sensing in a Nutshell

In signal processing the standard approach consists in determining an orthonormal basis of L2, for instance the Fourier basis for band-limited periodicically extendable signals or some wavelet basis. Then, employing the celebrated Nyquist-Shannon theorem a sampling rate that is at least twice the signal bandwidth is required. Such a sampling rate, nevertheless, may be unnecessarily high.

Compressed sensing is a signal processing methodology for the reconstruction of sparsely sampled signals and it offers a new paradigm for sampling signals based on their innovation, that is, the minimum number of coefficients sufficient to accurately represent it in an appropriately selected basis. Compressed sensing leads to a lower sampling rate compared to theories using some fixed basis and has many applications in image processing, medical imaging and MRI, photography, holography, facial recognition, radio astronomy, radar technology and more.

The traditional compressed sensing approach is naturally offline, in that it amounts to sparsely sampling and reconstructing a given dataset. Recently, an online algorithm for performing compressed sensing on streaming data was proposed (Freris et al., 2013): the scheme uses recursive sampling of the input stream and recursive decompression to accurately estimate stream entries from the acquired noisy measurements.

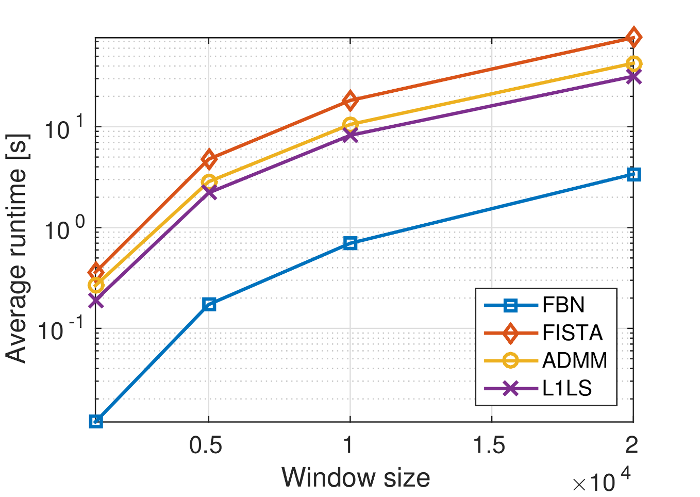
In this work we developed a recursive compressed sensing algorithm which makes use of a Forward-Backward Newton (FBN) method to efficient solve the involved LASSO problems in real time. Our simulations showed significant speed-up compared to all well-established algorithms for such problems such as (F)ISTA, ADMM and the L1LS algorithm by Kim et al (See Figure 1). Exploiting the fact that in recursive LASSO the optimizer at time k can be used to produce a good estimate at time k+1, and using the fact the FBN converges to the solution locally quadratically, at every sampling time we only need to perform a few Newton iterations.

Details about this work can be found in (Sopasakis et al., 2016).

Results

The remarkable speed-up of the proposed algorithm is a result of two factors: first it is the local quadratic convergence rate of the Newton method in combination with the warm start. Second, several terms such as the residual (i.e., the term Ax-y) and certain Cholesky factorizations can be passed to the next instance of FBN; this saves a considerable number of FLOPS at every iteration.

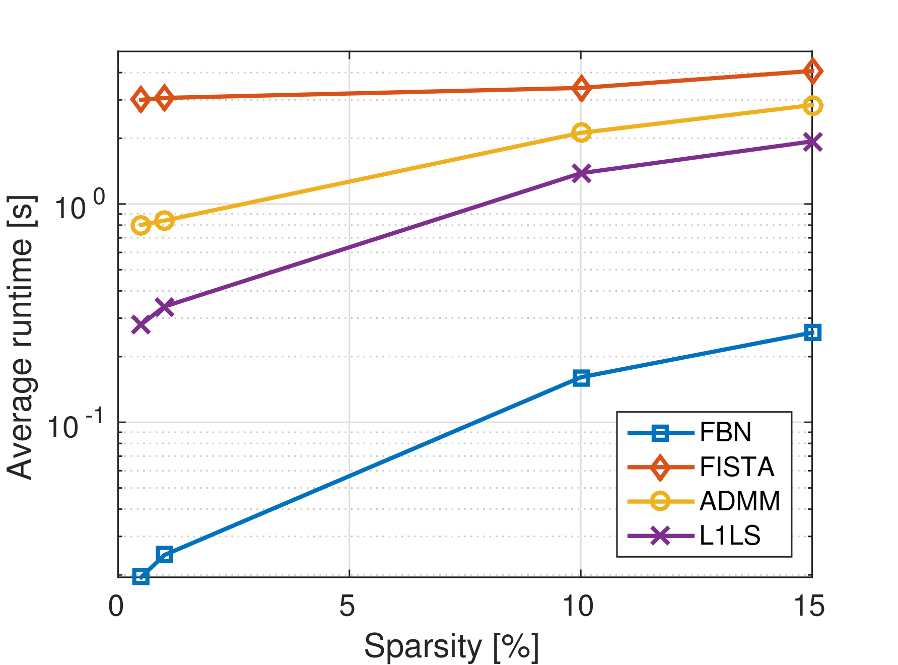
We have conducted several experiments varying the window size, the sparsity of the data strem, the required solution tolerance and the signal-to-noise ratio. In all cases and for a wide range of paramters, the proposed algorithm was found to be an order of magnitute faster than ISTA, FISTA, ADMM and L1LS. In Figure 1 we see in a logarithmic plot how the average runtime required to solve the L1-regularized least-squares problem varies with the window size (which is equal to the number of columns of matrix A). In Figure 2 we show how the sparsity of the data stream affect the average runtimes.

Details about how matrix A was selected and how the stream was generated can be found in (Sopasakis et al., 2016).

RCS comparison
Average runtimes varying the window size. FBN: proposed forward-backward Newton method, L1LS (Kim et al., 2007), ADMM (Afonso et al., 2010), FISTA (Beck and Teboulle, 2010). The proposed method is faster by an order of magnitude compared to other methods.
RCS sparsity
Average runtimes varying the sparisty of the data stream.

Acknowledgement

This work was financially supported by the EU under the H202 research project DISIRE, grant agreement no. 636834.

References

  1. P. Sopasakis, N. Freris and P. Patrinos, "Accelerated reconstruction of a compressively sampled data stream", European Signal Processing Conference 2016, Budapest, Hungary (submitted).
  2. N. Freris, O. Ocal and M. Vetterli, "Recursive compressed sensing," arXiv:1312.4895, Dec. 2013.
  3. S.-J. Kim, K. Koh, M. Lustig, S. Boyd, and D. Gorinevsky, "An interior-point method for large-scale l1-regularized least squares," IEEE Journal of Selected Topics in Signal Processing, vol. 1, no. 4, pp. 606–617, 2007.
  4. A. Beck and M. Teboulle, "A fast iterative shrinkage-thresholding algorithm for linear inverse problems," SIAM Journal on Imaging Sciences, vol. 2, no. 1, pp. 183–202, 2009.
  5. M. Afonso, J. Bioucas-Dias, and M. A. T. Figueiredo, "Fast image recovery using variable splitting and constrained optimization," IEEE Transactions on Image Processing, vol. 19, no. 9, pp. 2345–2356, 2010.
  6. P. Patrinos, L. Stella and A. Bemporad, "Forward-backward truncated Newton methods for convex composite optimization", arXiv:1402.6655, Feb. 2014.